Geometric Method for calculating Price Elasticity

(Linear Demand Curve)

Geometric method measures price elasticity of demand at different points on the demand curve.
It is also called ‘point method’ of measuring elasticity of demand.
We would be using linear demand curve, which is a straight line demand curve.
As shown in the below graph :

linear demand curve

MN is a straight line demand curve sloping downwards.

P is a mid point on the demand curve.
It divides the demand curve into two equal segments,
lower segment (PN) and upper segment (PM)
PN = Line segment below the point on  the demand curve

PM =  Line segment above the point on the demand curve

e_p(at P)  = PN / PM

Price Elasticity of demand at different points on Straight line Demand Curve

We can use the above mentioned method of point elasticity in measuring elasticity at different  points on a straight line demand curve starting from Y axis and terminating at X axis.

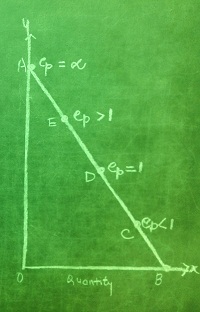demand curve

Following situation is evident from above graph using the above formula:

1) At point A (touches y axis)

e_p (at A)  = AB / 0 = infinity (∞)

2) At any point above the midpoint but below A, say at point E

e_p (at E)  = BE / EA > 1

Because the lower segment is greater than the upper segment, i.e. BE > EA

3) At the midpoint D

e_p (at D)  = BD / DA = 1

Because the lower segment is equal to upper segment, i.e. BD = DA

4) At any point below the midpoint but above B, say at C.

e_p (at C)  = BC / CA < 1

Because the lower segment is smaller than the upper segment, i.e. BC < CA

5) At point B (touches X axis)

e_p (at B)  = 0/ AB = 0

Hence we can generalize that a straight line demand curve is more elastic towards its left hand end and less elastic towards the right hand end.